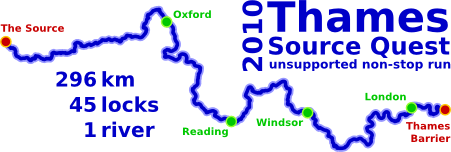
I've been spending quite a bit of time to try to estimate my speed on the
TSQ. The time I'll take to complete the challenge will not only determine the amount of food I'll need to carry, but also the ideal starting time that would minimise night running and enable me to catch a train back promptly.
1. Completion time
Unfortunately, it is really hard to estimate how long I will take to run the whole path. I've spend quite a bit of time developing a spreadsheet to simulate the run with linear and logarithmic speed decrease. The results are not very satisfactory because I've not got much to compare with, and therefore the split time estimation evaluation is a bit random. The longest I've run in similar conditions was London-Brighton, which is only 90km, not even a third of the TSQ!
The Hardmoors 110 and the UTMB could provide a better estimation on the long-term but the nature of the underfoot conditions and the ascent makes any comparison difficult. We could use the
Naismith's rule (1892) to evaluate the impact of the ascent on the overall speed:
1 hour for every 3 miles forward, plus 1/2 hour for every 1000 feet of ascent.
This would lead us to consider 3 miles (5km) flat equivalent to 2000 feet (600m), in other words 120m of ascent worth 1km flat. In this case, the UTMB 2007 would be equivalent to 163+8900/120=237km on a flat surface and the Hardmoors 2008 to 177+5700/120=224km. This would lead to a finish time of about 45 to 48 hours on the TSQ, but I'm not sure to what extend this kind of estimation is valid.
Also, there are very few races of that sort of length out there to see how other runners might perform. The Thames Path Ring (250miles) is one of them. The runners passed at checkpoint 7 (a convenient 295km) between 43 and 64 hours, with a large majority (12/14) between 55 and 64 hours. Looking at these results, it would be rather optimistic to think I could complete the TSQ in much less than 50 hours.
Considering these two cues, I'm targeting to complete the TSQ in 48 hours, but wouldn't be surprised to take up to 6 hours more or less than that... I was hoping for a bit less (and therefore a single night out), but that's probably not going to be possible. Using the logarithmic speed decrease model, 48 hours can be achieved by starting at 9.5km/h and dropping roughly 2.6% per 10km, that's a finishing speed of only 4.3km/h :) . Manageable.
2. Starting time
Given the large uncertainty in the finishing time it's not easy to optimise my starting time. On one hand, I will run through two nights if I take 48 hours, whatever the starting time. That said, if I start (and therefore arrive) at dawn (04:00), every hour faster than 48 hours will be deduced from night time and every hour slower will be added to daylight time, which is optimal. On the other hand, given that the trains roughly run between 10:00 and 22:00 on Sundays, I should really target to arrive (and therefore leave) at 16:00, leaving a safety margin of 6 hours either way. 04:00 or 16:00? The two optimal solutions are diametrically opposed! Maybe I should just go for it without thinking to much and improvise on the way?
This is the resulting spreadsheet on which I spend quite a bit of effort. On the way, I increased my astronomical knowledge in order to automatically calculate the day/night/twilight parameters at a given date, time and location :) .
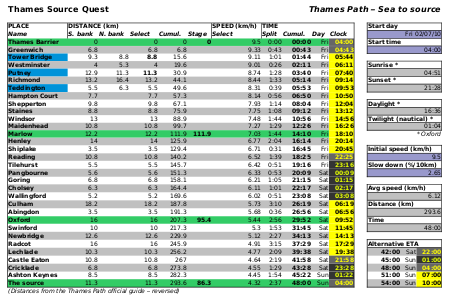
Click for the PDF full version
As for the pace, I'm considering using a 9/1 run/walk strategy from the start,
ie. 9 minutes running and 1 minute walking. This has been proven effective to reduce muscle fatigue on the long term, and therefore reduce the slow down coefficient.
3. Route
There is a bit of a choice in terms of route, as the path runs on both sides of the River in London. I've mostly chosen the shortest options :) . Not because they are shorter, but because they are closer to the river and therefore propose a "purer" line as well as being easier to navigate. This is especially true in the docklands and around Battersea.
At Weybridge the regular path is relying on a small ferry to cross the River. An alternative bridge option makes a detour away from the river and adds about 2km. When running upstream, I'll have to decide between the two options 2km ahead of the ferry crossing,
ie. at Walton Bridge. If at that point I decide to go for the shortest 2km option but the ferry doesn't actually run, I'll have to run back to the bridge option for a total of 8km. If I decide to go for the bridge straight away, it's 4km. In short, that's a guaranteed 4km or a bet between 2km and 8km. Tricky...
4. Mapping
I've mapped the whole path on Memory-Map (1:25,000) and generated 45 A5-size cards, as illustrated hereafter. I have to say it took a while to generate a decent result. This is because the Memory-Map software can't automatically section a route into cards*. You have to position (and sometimes rotate by 90 degrees) manually the boundaries of every single card without being able to see the other ones... I'll probably leave aside the central London sections and print 40 cards on tough paper, that is only 10 A4-size double-sided sheets.
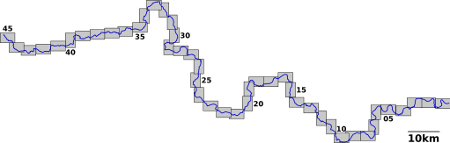
Money-wise, it comes out a bit more expensive than slicing the regular OS maps but cheaper than the laminated ones:
| Memory-Map | OS Explorer | OS Explorer Active (laminated) |
|---|
Memory-Map Thames Path: £100.00
Thoughprint**: £6.00 |
160, 161, 162, 168, 169, 170, 171, 172, 173, 180: £7.99 each |
160, 161, 162, 168, 169, 170, 171, 172, 173, 180: £13.99 each |
| Total: £106.00 | Total: £79.90 | Total: £133.90 |
I guess I've done enough homework... Just need to run now :)
Ultra logistics
* I've written a 27-line Python script that does the job rather well (it generates 43 cards, but with strictly no overlap), but I have no way to integrate it into Memory-Map...
** £14.99 for 25 sheets